Introduction

K-Nearest Neighbors (KNN) is a supervised classification algorithm. Now let's break down the name. "Supervised" means it requires labels or correct outputs to be known for the training data. "Classification" means it divides the dataset into two or more classes.

The working of KNN is quite simple. For a test point, we check what other points are closest to it. It is like an imaginary boundary around the test point and the points inside this boundary are called its Nearest Neighbors. This boundary is defined by the "k" value i.e. the number of nearest neighbors we're considering for the point.

In the figure below we graph points in two classes. We see the boundary around the test point is determined by the value of "k", which is 5 in this figure.

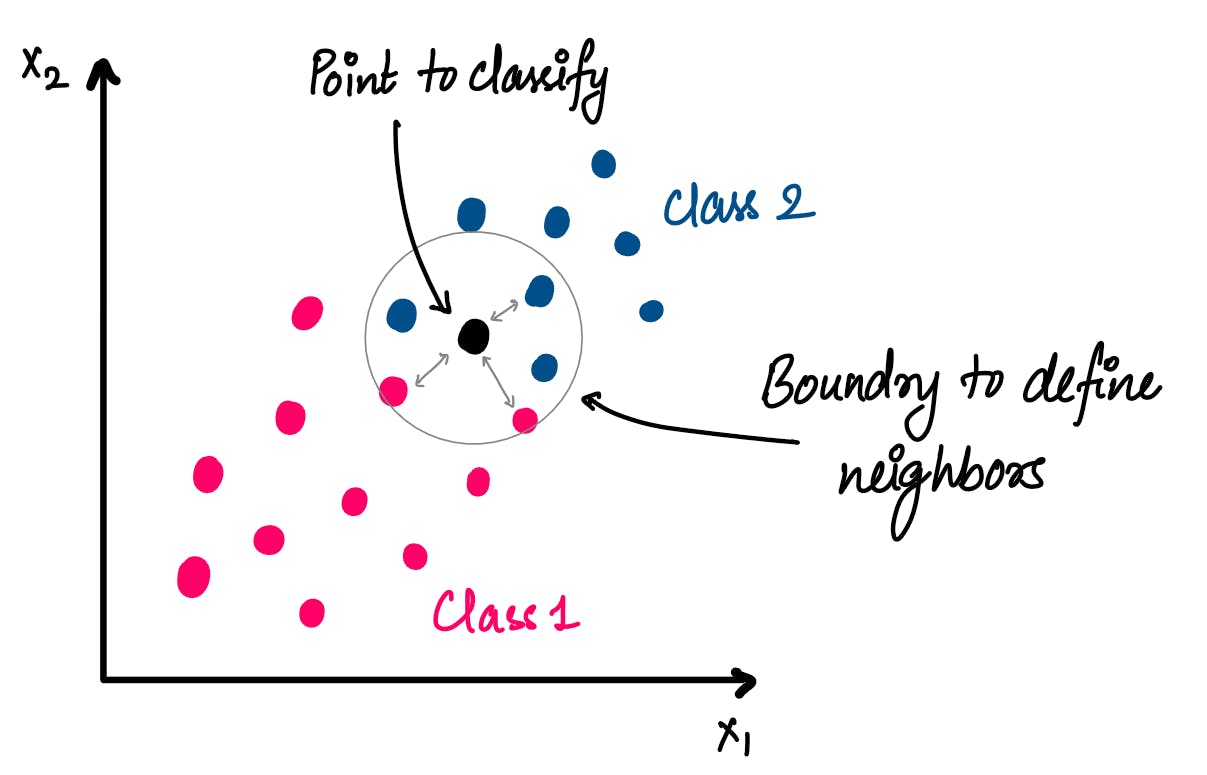
Once we have the closest "k" points to the test point, we have a voting system where each point votes for its own class and the class with the highest votes is assigned to the test point.

KNN is also a lazy classifier as it requires all the points in the dataset to be present when we try to predict a new point.

Recipe

Let us now define the KNN algorithm in form of a simple recipe (just like a cookbook!).
If you already know the concepts and want to skip directly to the code, go to the last section titled "Complete Code".

Every recipe can be divided into the following sections:

Ingredients: These are usually our data and its pre-processing steps to make it suitable for our algorithm.
Equipment: It is the actual working of the algorithm.
Direction: Applying the algorithm to our data and testing it for required performance (tasting the dish 😋).

Ingredients

We might cheat here a little bit and get some data from a well-known Python library "scikit-learn". Unless by making a recipe by scratch you also mean you grow the ingredients yourself, I believe this is acceptable.

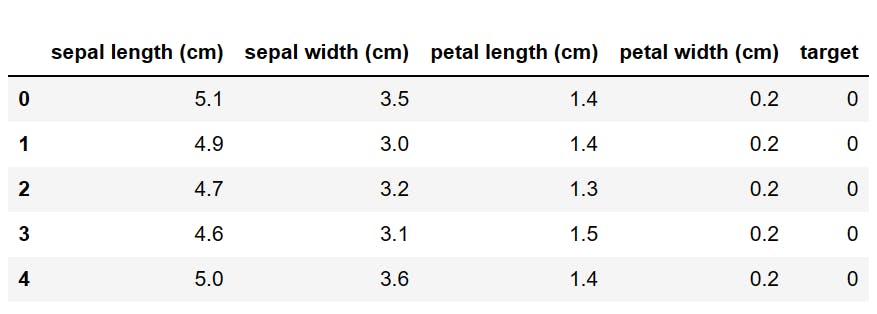
We load the Iris Dataset, which contains 3 classes - Setosa, Versicolor and Virginica.
But for simplicity, let's just call them class 0, 1 and 2 respectively. These classes have four features - sepal length and width, petal length and width (all in cm).

from sklearn import datasets
import pandas as pd

iris = datasets.load_iris()

# Loading iris dataset into our Pandas Dataframe
dataset = pd.DataFrame(data=iris.data, columns=iris.feature_names)
dataset['target'] = iris.target

We can view the top of our dataset using dataset.head() and we obtain the following result.

Next, we divide our dataset into Training and Test splits. With this, our ingredients for the recipe are ready!

import random
from math import floor
import numpy as np

def split_dataset(dataset, test_size):
    # Shuffling our dataset to remove any bias
    df = dataset.sample(frac=1)

    X = df.drop('target', axis=1)
    y = list(df['target'])

    # Calculating the point of split in the dataset
    pivot = floor(len(X) * (1-test_size))

    # Points before the pivot go to training set, rest to testing set
    X_train = np.array(X.iloc[:pivot,:])
    X_test = np.array(X.iloc[pivot:,:])

    y_train, y_test = y[:pivot], y[pivot:]

    return X_train, X_test, y_train, y_test

X_train, X_test, y_train, y_test = split_dataset(dataset, test_size=0.25)

Equipment

The most important part of the KNN Recipe is the concept of distinguishing one point from another. We use the concept of distance between two points to see how similar or different they are.
One of the most common distances used is Euclidean distance. It is the geometric distance between the points(vectors) given by the formula:

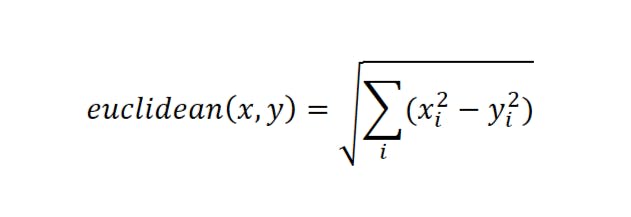
where 'i' denotes each dimension of vectors x and y.

We implement the Euclidean distance as follows:

from math import sqrt

def euclidean_dist(vec1, vec2):
    distance = 0
    dimen = len(vec1)

    # For each dimension, we calculate the square of difference
    for i in range(dimen):
        distance += (vec1[i]-vec2[i])**2

    return sqrt(distance)

Note that we can also have other types of distance metrics, but that would be for a more professional cook 👨‍🍳

Now we calculate the Euclidean distance from our test point to every other point in the training set and sort the points in non-decreasing (fancy ascending) order.
Next, we only take the top "k" values as our nearest neighbors.

def find_neighbors(point, X_train, y_train, k):
    distances = list()

    # We save points with their classes and distances
    for i in range(len(X_train)):
        distance = euclidean_dist(point, X_train[i])
        distances.append((y_train[i], distance))

    # Sorting the list by the distances    
    distances.sort(key=lambda x:x[1])

    # we save the classes of top "k" points in neighbors
    neighbors = list()
    for i in range(k):
        neighbors.append(distances[i][0])

    return neighbors

Directions

Now, it is finally time to make the dish using the ingredients and equipment.

First, for each point in the testing dataset, we find out the nearest neighbors. These neighbors are the top "k" points to the test point.
Second, for each class, we count the neighbors present, and the class having the maximum number of neighbors will be assigned as the class of test point.

def knn_classifier(X_train, X_test, y_train, y_test, k):
    y_hat = list() # to save all predictions

    # Calculate for each test point
    for i in range(len(X_test)):

        # Finding top "k" neighbors of the point
        neighbors = find_neighbors(X_test[i], X_train, y_train, k)

        # Saving the class with maximum votes as predicted class
        prediction = max(set(neighbors), key = neighbors.count)
        y_hat.append(prediction)
    return y_hat

y_hat_test = knn_classifier(X_train, X_test, y_train, y_test, 5)

Tasting (Testing?)

Now to check how good our recipe is i.e., how good our model performs, we calculate the accuracy of the model.

We assign the value 1 for each correct match and sum these up to get the total number of correct predictions. Then we divide the correct matches by the total number of samples in our testing data.

def accuracy(actual, predicted):
    correct  = sum([1 for i in range(len(actual)) 
                          if actual[i]==predicted[i] ])
    return correct/len(actual)

print(accuracy(y_test,y_hat_test))

We obtain an astounding accuracy score of 0.9474 i.e. 94.74%, which in my opinion is amazing. But if my word isn't enough let's check what "best-in-class" KNeighborsClassifer in scikit-learn library performs!

from sklearn.neighbors import KNeighborsClassifier
from sklearn.metrics import accuracy_score

clf = KNeighborsClassifier(n_neighbors=5, p=2)
clf.fit(X_train, y_train)
y_pred_test = clf.predict(X_test)

print(accuracy_score(y_test, y_pred_test))

This ALSO gets an accuracy score of 0.9474 which is the same as our classifier! WOW!

Complete Code

In case you already knew the concepts and wanted single concise code, here you go!

from sklearn import datasets
import pandas as pd
import random
from math import floor, sqrt
import numpy as np

# ----- Preparing Training and Test Datasets ----- #
def split_dataset(dataset, test_size):
    df = dataset.sample(frac=1)
    X = df.drop('target', axis=1)
    y = list(df['target'])
    pivot = floor(len(X) * (1-test_size))
    X_train = np.array(X.iloc[:pivot,:])
    X_test = np.array(X.iloc[pivot:,:])
    y_train, y_test = y[:pivot], y[pivot:]
    return X_train, X_test, y_train, y_test

# ----- Calculating distance between points ----- #
def euclidean_dist(vec1, vec2):
    distance = 0
    dimen = len(vec1)
    for i in range(dimen):
        distance += (vec1[i]-vec2[i])**2
    return sqrt(distance)

# ----- Finding k closest points ----- 
def find_neighbors(point, X_train, y_train, k):
    distances = list()
    for i in range(len(X_train)):
        distance = euclidean_dist(point, X_train[i])
        distances.append((y_train[i], distance))      
    distances.sort(key=lambda x:x[1])
    neighbors = list()
    for i in range(k):
        neighbors.append(distances[i][0])
    return neighbors

# ----- Predicting class based on highest vote by neighbors ----- #
def knn_classifier(X_train, X_test, y_train, y_test, k):
    y_hat = list()
    for i in range(len(X_test)):
        neighbors = find_neighbors(X_test[i], X_train, y_train, k)
        prediction = max(set(neighbors), key = neighbors.count)
        y_hat.append(prediction)
    return y_hat

# ----- Calculating accuracy of the model ---- #
def accuracy(actual, predicted):
    correct  = sum([1 for i in range(len(actual)) 
                          if actual[i]==predicted[i]])
    return correct/len(actual)


# --------------- MAIN PROGRAM EXECUTION --------------- #

# ---- Getting data and creating splits ----- #
iris = datasets.load_iris()
dataset = pd.DataFrame(data=iris.data, columns=iris.feature_names)
dataset['target'] = iris.target
X_train, X_test, y_train, y_test = split_dataset(dataset, test_size=0.25)

# ----- Applying KNN algorithm and calculating accuracy ----- #
y_hat_test = knn_classifier(X_train, X_test, y_train, y_test, 5)
print(accuracy(y_test,y_hat_test))

Simple K-Nearest Neighbors Recipe

Building K-Nearest Neighbors Classifier from Scratch

Table of contents